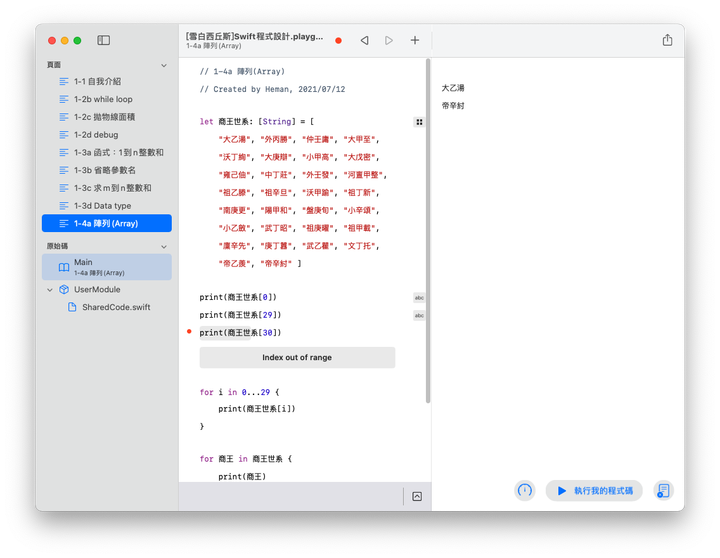
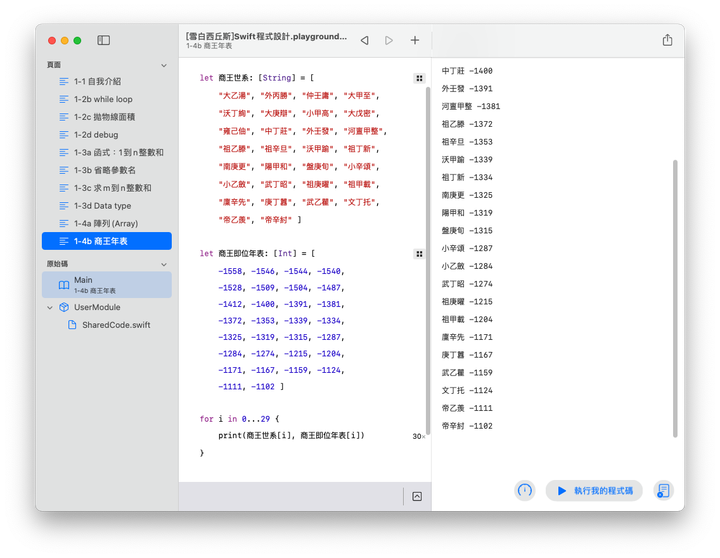
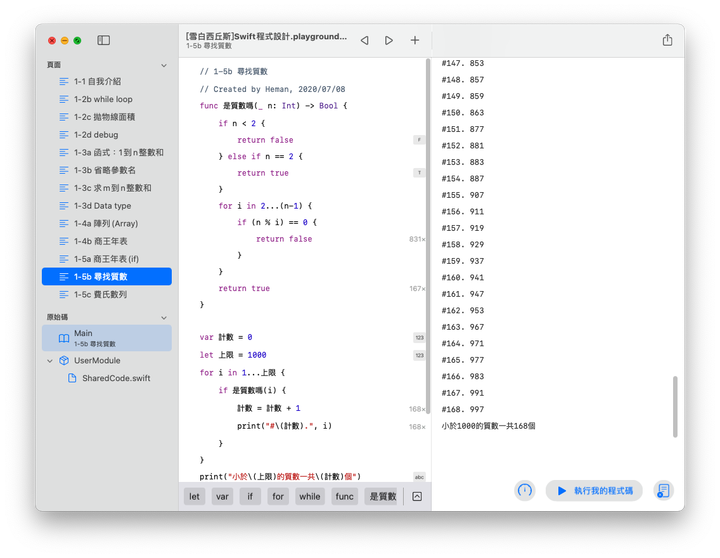
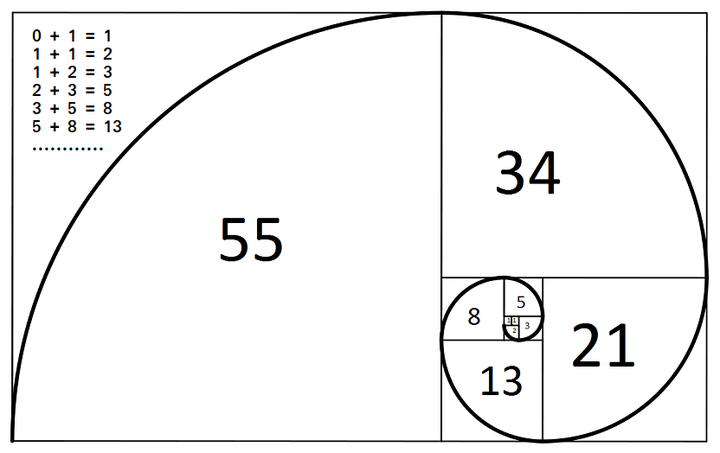
以Swift設計的程式,基本上可以簡化為「資料」與「指令」所構成,前兩課的範例中,我們用 let, var 來定義資料,用等號 = 來指定資料值,用 + - * / 來做資料運算;用 print() 指令來輸出字串,用 for, while 等迴圈指令來重複執行程式片段,資料與指令的適當組合,以完成某些工作,就構成一個程式。
我們會學到很多Swift預先設計好的指令,除此之外,我們還可以自行定義新的指令,也就是新的函式。函式原文是 function,跟數學的函數是同一個字,意思也大同小異,函式或函數都需要傳入參數,然後經過一段運算,得到一個結果。
例如我們第2課教過的1到100的整數和,如果我們想設計一個函式來計算1到任意數n 的整數和,該如何做呢?
// 1-3a 函式(func): 1到任意數n的整數和
// Created by Heman, 2021/07/09
func 整數和(n: Int) -> Int {
var 累計值 = 0
for i in 1...n {
累計值 = 累計值 + i
}
return 累計值
}
let x = 整數和(n: 1001)
print(x)
1-3a 範例中,我們定義了一個新函式:整數和(),接受一個參數名稱為 n 的整數,計算結果會傳回一個整數,函式本體 { } 裡面的程式碼,則幾乎跟範例1-2a一模一樣,只是將100改成可變的參數n。
所以定義函式的語法類似這樣:
func 整數和(n: Int) -> Int { }
通用的語法像這樣:
func 函式名稱(參數1: 資料類型, 參數2: 資料類型, ...) -> 回傳值的資料類型 { }
函式可以接受多個參數或完全不要參數,視需要來定義,如果完全不要參數,小括號 () 還是不可少,在上例中我們只需要一個參數。
當使用函式的時候(稱為函式呼叫 "Function Call"),只要在「函式名稱()」填入參數名稱與參數值,就會得到計算結果(回傳值),例如:
let x = 整數和(n: 1001)
令 x 等於 1 到 1001 的整數和。
什麼時候需要自訂函式?在第2課,我們只想要算1到100的整數和,因為這是高斯的經典問題,是特例,到了本課,我們想要推廣求1到任意數的整數和,變成通用的算法,所以函式可看成一種通用化的工具。
不過,如果參數只有一個的時候,呼叫時還要寫出參數名稱有點笨,下面例子提供一個偷吃步。
// 1-3b 函式(func): 參數名稱省略
// Created by Heman, 2021/07/09
func 整數和(_ n: Int) -> Int {
var 累計值 = 0
for i in 1...n {
累計值 = 累計值 + i
}
return 累計值
}
let x = 整數和(1001)
print(x)
函式宣告時,參數名稱前面的底線符號 _,具有「可省略」的意思,函式可以有一個或多個可省略參數(呼叫時不寫參數名稱),但必須寫在一般參數之前。這樣,函式呼叫的時候,從 整數和(n: 1001) 改成 整數和(1001) 是不是稍微順眼一點?
我們還可以進一步再推廣這個函式的用途:求 m 到 n 的整數和。
// 1-3c 函式(func): 求m到n整數和
// Created by Heman, 2021/07/09
func 整數和(m: Int = 1, _ n: Int) -> Int {
var 累計值 = 0
for i in m...n {
累計值 = 累計值 + i
}
return 累計值
}
let x = 整數和(1001)
let y = 整數和(m: 101, 1001)
print(x, y)
注意 func 定義時,參數名稱 m 額外加了一個「預設值」m: Int = 1,也就是說,定義函式時,參數若指定預設值的話,函式呼叫時,該參數就可以整個省略,例如 x = 整數和(1001),這時候 m 就會用預設值,計算1到1001的整數和。
函式的參數預設值沒有限制數量,可以每個參數都有預設值,純粹視需要而定。
當然,若要計算中間一段,如101到1001的整數和,就呼叫「整數和(m: 101, 1001)」即可。所以相當於這個函式有兩種呼叫方法,這樣通用性就更好了。