#書籍推薦
#公式之美:23個經典公式,掌握宇宙萬物法則,喚醒你的數學魂
作者: 量子學派, 羅金海
出版社:漫遊者文化
出版日期:2022/11/02
目錄
序
前言
【理論篇】
1 1+1=2 :數學的溯源
2 畢氏定理:數與形的結合
3 費馬大定理:困擾人類 358 年
4 牛頓 - 萊布尼茨公式:無窮小的秘密
5 萬有引力:從混沌到光明
6 歐拉公式:最美的等式
7 伽羅瓦理論:無解的方程
8 危險的黎曼猜想
9 熵增定律:寂滅是宇宙宿命?
10 麥克斯韋方程組:讓黑暗消失
11 質能方程:開啟潘朵拉的魔盒
12 薛丁格方程:貓與量子世界
13 狄拉克方程:反物質的「先知」
14 楊-米爾斯規範場論:大統一之路
【應用篇】
15 向農公式:5G 背後的主宰
16 布萊克-斯科爾斯方程:金融「巫師」
17 槍械:彈道裡的「技術哲學」
18 胡克定律:機械錶的心臟
19 混沌理論:一隻蝴蝶引發的思考
20 凱利公式:賭場上的最大贏家
21 貝葉斯定理:AI如何思考?
22 三體問題:揮之不去的烏雲
23 橢圓曲線方程:比特幣的基石
人物索引
...
大陸出版的簡體文。
公式之美
轉貼文件:
序 公式鑄就 文明天梯
1854年之前,歐洲數學家燦若星辰,笛卡兒、拉格朗日、牛頓、貝葉斯、拉普拉斯、柯西、傅里葉、伽羅瓦等,無一不是數學天才。
1854—1935年,高斯、黎曼等人在數學界領袖群倫,德國取代英法成為世界的數學中心。
1935年之後,希特勒給美國送上“科學大禮包”:哥德爾、愛因斯坦、德拜、馮•諾依曼、費米、馮•卡門、外爾……很多科學家逃至北美,數學大本營從德國轉向美國,美國成為世界的數學中心。
每一次數學中心的交替,都是文明中心的變換,可見,文明造就數學,數學推動文明,兩者相輔相成。
回溯過去,人類自第一次領悟1+1=2的原理,便擁有了樸素的數理思維,這也標誌著人類開始搭建文明的階梯。這塊階梯舉足輕重,它是文明的基石。
當古人開始用數理知識總結自然規律時,文明的進化便由此啟程。人類從石器時代走進農耕時代,又從工業時代跨入資訊時代,數學是不可或缺的“第一功臣”,而公式則是這位功臣手中最鋒利的劍。
人本不過是宇宙中的一粒塵埃,卻能洞見宏大宇宙之真諦。
如果我們將人類視為文明個體,那麼公式則凝聚著人類頂尖的智慧。當人類步履匆匆來到這個宇宙,最終又不得不離去之時,當肉體歸為塵埃,隨風飄散的時候,唯有公式,成了人類文明在宇宙存在過中的見證。
公式是充滿智慧的,同樣也是美的。歐拉公式中的五大常數、混沌定理中飛舞的蝴蝶、斐波那契數列中的黃金螺旋線……公式的美不是外表的繁華與曇花一現,而是內在的永恆。
一片落葉飄落,就是一段美妙的函數方程,
沒有什麼能比公式更動人地描繪宇宙之美。
在剛剛被邀請為此書作序時,我心中頗受觸動!
作為一個數學愛好者,深知出版這樣一本書的不易。每一個公式就是一門學科,每一個公式就是一個世界,書中所提及的公式不僅涵蓋代數、群論、數論、微積方程、幾何拓撲學、非歐幾何等多個數學分支,還跨越了力學、熱力學、電磁學、相對論、量子力學、天體物理等自然學科,並囊括了電腦、AI、區塊鏈等前沿領域。
《公式之美》用既專業又有趣,既嚴謹又通俗的語言,向我們展示“公式之美”,既要照顧專業,又要普及大眾,非常不容易。
在這個越來越浮躁的時代,公式是重塑時代理性最重要的知識之一。只要還有人相信公式鑄就了人類智慧攀升的天梯,就代表文明的天梯可以無限延展下去。
北京大學數學科學學院教授,北京數學會理事長
公式之美
前言 人類的墓誌銘
萬物速朽,唯有公式永恆;
人間虛妄,數學是唯一真理;
存在即數,0和1統治一切;
大道至簡,數是最美的語言......
哥廷根是德國薩克森州的一座小城。它佔地120平方千米,有13萬居民。這座小有名氣的「花都」,曾經是數學世界的「麥加」。哥廷根小城有一個墓園,是科學愛好者眼中的「聖地」。在這小小的墓園裡,長眠著數位優秀科學家。走近這個小世界,人能一瞬間變得安詳、靜穆,不再有任何雜念。
第一次來到哥廷根,穿越萊納河,拜訪雅可比教堂,瞻仰高斯雕塑,本以為已經走進了這座城市的歷史深處,了解了它的內心世界——它的沉默和嚴謹讓它站在了19世紀的學術巔峰,它的深刻和純粹使它成為20世紀的數學莊園。
然而,只有走近這片回蕩著數學余韻的墓地,看到這些刻著符號的墓碑,讀懂上面的銘文後才明白,為什麼這座面積不足中國香港1/9的小城會在科學史上留名,會吸引足足45位諾貝爾獎得主在此學習、研究、思考......最後長眠於此。
相比帝王陵寢,這裡的墓碑並不恢宏。然而,只要你認真觀察,你會被一塊塊墓碑上的墓志銘所震撼。奧托•哈恩墓碑上的核反應公式,玻恩墓碑上的波函數概率分析,普朗克墓碑上的量子力學常數值......每一道墓志銘背後,隱藏的都是一段輝煌人生。
這些靈魂的偉大難以用文字來描述,每段人生都仰之彌高。唯有由數字、字母組成的極簡符號,即天書一般的公式,才能匹配他們的不朽。
可能有人會質疑,這些數字符號既不能果腹,也不能消遣,還有一些公式至今毫無用處,何以經得起如此之高的贊譽?是的,歐拉公式看似完美,實用性卻不強;三體問題爭論百年,至今懸而未決;還有更多公式始終讓人不明所以......但這些貌似「無用」的公式才是人類至寶。
古希臘幾何學家阿波洛尼烏斯總結了圓錐曲線理論,一千多年後,德國天文學家開普勒才將其應用於行星軌道;高斯被認為最早發現非歐幾何,半個世紀後,由他弟子創立的黎曼幾何成為廣義相對論的數學基礎。伴隨著槓桿原理、牛頓三大定律、麥克斯韋方程、香農公式、貝葉斯定理等,人類向蒸汽時代、電力時代、信息時代乃至人工智能時代徐徐邁進。
此時,雨還在下,墓園十分幽靜,僅有的一座禮堂也被綠蔭遮蔽。沿著綠蔭大道,走到藤蔓茂盛的蓮花池邊,諾貝爾獎得主普朗克、哈恩、海森堡、勞厄和溫道斯的墓碑一字排開,而極具爭議的科學家海森堡只有一塊紀念碑,他曾經的老師玻恩則靠近墓園東南角,似乎不太願意與這位弟子待在一起。此地還有無數先賢和隨行的痴者,同伴試圖找到狄利克雷、克萊因、希爾伯特、外爾和閔可夫斯基的墓碑,但墓碑在林間散落,難以一一辨別。
直面每一座墓碑上的公式,聆聽到的都是高維的回聲。雖有綠蔭掩映、雜草共生,但沒有什麼能遮蓋這無與倫比的光芒。
回首人類文明,人類如果在熱寂的宿命裡要給自己建立一座墓碑的話,那墓碑上應該鐫刻些什麼呢?毫無疑問,一定是某個公式。
至於到底是選擇牛頓的萬有引力定律公式,還是量子世界的薛定諤方程;是開創電磁時代的麥克斯韋方程組,還是洞察宇宙的愛因斯坦質能方程;是接近大統一理論的楊•米爾斯方程,還是放之四海皆准的熵增定律公式,每個人都有自己的答案。但無論是以上哪個公式,它們都會向整個宇宙訴說:在廣袤的宇宙中,有一個位於銀河系邊緣第三旋臂——獵戶臂上的藍色星球,這顆星球上存在的智慧種族,發現了宇宙的規律。
理論篇
1 1+1=2:數學的溯源

數學獨立於時空之外,在哪個宇宙都是亙古不變的。

從遠古說起
在遠古時期,兩個古埃及人若是在尼羅河捕到了3條魚,那會是他們一天中最幸福的時刻。因為在物資極其匱乏的原始部落裡,3是他們能想到的最大的數字。如果一個數字大於3,他們的腦袋就會變成一團亂麻,只能回答「許多個」或者「數不清」。但很快,這兩個古埃及人開始苦惱起來,香氣撲鼻的烤肉味使他們在心中打起了小算盤。兩人偷偷地擺弄起自己的手指計數:每人一條魚,那就是丨和丨,擺在一起顯然是丨丨,那剩下的魚怎麼辦呢?
將它帶回去贈給年逾古稀的酋長,還是獻祭給護佑部落的法老,或者直接丟回尼羅河,讓它回歸自己的故鄉?
第3條魚宿命如何,我們不知道,但是在分配食物的過程中,祖先在有了「數量」的概念之後,逐漸意識到了1+1=2,這看似小兒科,卻是人類文明史上極其偉大的時刻。因為在祖先認識到兩數相加得到另一個確定的數時,已經具備了超越其他種族的數學思維,並且發現了「數學」的一個重要的性質——可加性。
1+1=2,關於這個公式,它直接涉及的就是加法和自然數 ① 。它看似簡單,卻是數學最原始的種子,有了這顆種子,數學這棵樹才開始生根發芽、茁壯成長,直至今天成為人類文明的基石之一。
加法和自然數
我們已經無從考證,加法究竟產生於何時,但從文字記載中發現,加法和減法運算是人類最早掌握的兩種數學運算。古埃及的阿默斯紙草書中就用向右走的兩條腿「 」表示加號,向左走的兩條腿「 」表示減號。目前通用的「+」「-」出現於歐洲的中世紀時期,當時酒商在售出酒後,曾用橫線標出酒桶裡的存酒,而當桶裡的酒增加時,便用豎線把原來畫的橫線劃掉,於是就出現「-」和「+」兩個符號。1630年以後,「+」作為運算符號得到公認。
自然數比「+」「-」出現得更早。大約在1萬年以前,冰河退卻的石器時代,馬背上的游牧狩獵者開始了一種全新的生活,他們從馬背上跳了下來選擇農耕,雖然吟游詩人一直在歌頌自由的游獵生活,但那只是表面的風光。實際上,尋找到一塊肥沃的土地定居下來,刀耕火種才能讓一個家吃飽穿暖,繁衍後代。
這是一種巨大的改變,與簡單粗暴的掠奪方式不同,他們需要掌握更多的數學知識,記錄季節和日期,計算收成和種子。這讓這群四肢發達的壯漢很是頭疼。
在尼羅河谷、底格裡斯河與幼發拉底河流域,很快就發展起了更復雜的農業社會,這群剛進入新時代的農民還遇到了交納租稅的問題。顯然,過去石器部落文化裡總結的「1、2、3」已遠遠不夠用了,人們迫切需要「數」有名稱,而且計數必須更准確。
然而,沒有人見過自然數,也沒有人知道它是怎麼排列分布的。
自然數是用以計量事物的件數或表示事物次序的數。它的分布或許是兜兜轉轉一個圈,或許是螺旋交錯纏繞式,或許是放射爆炸發散式......不同的選擇就會有不同的結果。數學最後選擇的是不可逆的直線式的有序體系,如圖1-1所示,自然數也有了統一的表現方式。

圖1-1 自然數
自然數和加法的出現,標志著人類有了自己的數學「橋頭堡」。從此,人類開啟了智力之路的漫漫長征。
皮亞諾的五條公理
我們都知道1+1=2,但你是否想過1+1為什麼等於2 ?
.................................(待續)
皮亞諾的五條公理
我們都知道1+1=2,但你是否想過1+1為什麼等於2 ?一旦思考這個問題,就會陷入無窮無盡的煩惱之中——只要涉及本質的追問,人類總是手足無措,就像我們追問宇宙大爆炸中誰是「第一推動力」一樣。
很多人會說,這個公式是無須證明、無須解釋的。但那些真理的信徒並不認為這是一個好答案,他們熱衷於「鑽牛角尖」:憑什麼1+1=2就不需要證明了?
有幾位數學家孜孜不倦地在探索中為我們解答了這一問題。其中,意大利數學家皮亞諾用公理 ② 把自然數安放在了數學世界中,用五條公理建立了一階算術系統,可以用來推導出1+1=2這一最簡單的等式。
公理1 :0是自然數。
茫茫的數學宇宙裡,從此有了第一個身影——0,如圖1-2所示。
圖1-2 0
公理2 :每一個確定的自然數a,都有一個確定的後繼數 ③ a′,a′也是自然數。
那麼,這個自然數起點0是怎麼爆發的呢?後繼數會以什麼樣的形式出現?是調皮地圍著0轉,還是偷偷地跑到0的後面,抑或是狠心地留0在那兒?公理2做出了選擇,讓偌大的數學空間中出現的每個數都擁有一個確定的後繼數陪伴著自己,如圖1-3所示。

圖1-3 後繼數
公理3 :0不是任何自然數的後繼數。
為了避免後繼數不守規矩跑到0的前面,公理3確定了0必須也只能是自然數的第一個數。但是防不勝防,這群後繼數也沒那麼安分,有可能2的後繼數2=3′,也可能3的後繼數3=3′,如圖1-4所示。
圖1-4 前後相繼(1)
公理4:不同的自然數有不同的後繼數。
為避免上述情況,公理4定義:如果n與m均為自然數且n≠m ,那麼n′≠m′;如果b、c均為自然數,且b′=c ′ ,那麼b=c。同一個自然數的後繼數相等,不同自然數的後繼數不相等。這樣,3就不可能既是2的後繼數,也是3的後繼數了。但如果出現圖1-5中2.5這樣的數呢?
圖1-5 前後相繼(2)
為了杜絕2.5這樣的非自然數出現,公理5出現了。
公理5 :假定P(n ) 是自然數的一個性質,如果P(0) 是真的,且假定P(n ) 是真的,則P(n′)也是真的,那麼命題對所有自然數都為真。
它還有另外一種表述形式。
設S是自然數集的一個子集,且滿足:(1)0屬於S ;(2)如果n屬於S,那麼n′也屬於S,則S是包含全體自然數的集合,即S=N。
這裡的說法可能會有點拗口,但皮亞諾是一個頗有潛力的「饒舌歌手」。其實這是數學中的歸納公理,也就是說,如果定義了一個自然數的性質,那麼所有自然數都將滿足這個性質,不滿足的就不是自然數。這樣,我們可以定義自然數系:存在一個自然數系N,當且僅當這些元素滿足公理1~5時,稱其元素為自然數。
然後,定義加法是滿足以下兩種規則的運算:
(1)對於任意自然數m, 0+m=m ;
(2)對於任意自然數m和n, n′+m=(n+m)′。
這樣,我們就可以證明1+1=2 :

或者
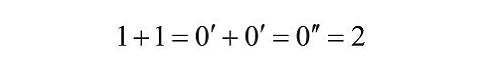
因為1+1 的後繼數是1的後繼數的後繼數,即3;又因為2的後繼數也是3,根據皮亞諾公理4,不同自然數的後繼數不同,反之,如果兩個自然數的後繼數相同,那麼這兩個自然數就相等,所以1+1=2。
這樣,根據皮亞諾五條公理建立起來的皮亞諾一階算術系統,我們就推導出了1+1=2。
哥德巴赫猜想另一個「1+1」
如何推導出1+1=2,數學家在自己的世界裡尋找到了一個相對滿意的答案,雖然有點「自欺欺人」,但總算放下了心裡的一塊石頭。然而,比這個更麻煩的,是解決世間另一個「1+1」,這才是歷代數學家的心頭之痛。哥德巴赫猜想是數學皇冠上一顆可望而不可即的「明珠」,堪稱世界近代三大數學難題之一。
在18世紀前後,德國一個富家子弟哥德巴赫厭倦了錦衣玉食的生活,於是在某個失眠的夜晚過後,不顧家人阻攔,跑去做了一名中學教師,還從此一發不可收地愛上了數學,就連晚上回家休息也在搗鼓阿拉伯數字。他生平最喜歡玩的游戲竟是加法運算,而且還在玩加法游戲的過程中發現了一個規律:任何大於5的奇數都是三個素數 ④ 之和。但令他無奈的是,他雖然發現了這個神秘的數學規律,卻怎樣也無法證明自己的發現。後來,他只能求助於當時數學界的權威人士歐拉。
1742年6月7日,哥德巴赫寫信給歐拉,提出任何大於5的奇數都是三個素數之和。隨便取一個奇數77,可寫成三個素數之和,77=53+17+7。再任取一個奇數461,461=449+7+5,也是三個素數之和;461還可以寫成257+199+5,仍然是三個素數之和。
沒想到數學家歐拉居然也被這個問題給難住了。1742年6月30日,歐拉給哥德巴赫回信:這個命題看來是正確的,但我也給不出嚴格的證明。為了挽回自己的面子,「狡猾」的歐拉同時還提出了另一個等價命題:任何一個大於2的偶數都是兩個素數之和。
這樣一個「任一充分大的偶數,都可以表示為一個素因子個數不超過a個的數,與另一個素因子不超過b個的數之和」的命題,就被記作a+b,哥德巴赫猜想(也稱哥德巴赫-歐拉猜想)也因此被稱為另一個「1+1」。迄今為止,這個「1+1」只留下一份如圖1-6所示的稀世手稿,而有關它的證明依然在困擾著數學界。

圖1-6 哥德巴赫猜想手稿
二進制世界裡的1+1
德國圖林根著名的郭塔王宮圖書館中有一份彌足珍貴的手稿,它的標題為:「1與0,一切數字的神奇淵源。這是造物秘密的美妙典范,因為,一切無非都來自上帝。」這是德國天才大師萊布尼茨的手跡,他用異常精煉的描述,展示了一個神奇美妙的數字系統——二進制。他告訴我們:1+1≠2,在計算機代碼的世界裡,1+1=10。
萊布尼茨在1697年還特意為「二進制」設計了一枚銀幣,如圖1-7所示,並把它作為新年禮物獻給他的保護人奧古斯特公爵。萊布尼茨設計此銀幣的目的是,以公爵的身份來引起人們對他創立的二進制的關注。

圖1-7 「二進制」銀幣的反面
銀幣正面是威嚴的公爵圖像,幽暗的瞳孔似乎在沉思什麼;反中間部分雕刻的是從1到17的二進制數學式。面則刻畫著一則創世故事——水面上籠罩著黑暗,頂部光芒四射……
二進制是計算機技術中廣泛采用的一種數制。二進制數據是用0和1兩個數碼來表示的。它的基數為2,進位規則是「逢二進一」,借位規則是「借一當二」。當前的計算機系統使用的基本上都是二進制系統,數據在計算機中主要是以補碼 ⑤ 的形式存儲的。
可以說,從20世紀第三次科技革命爆發以來,人類就進入了計算機時代,我們在虛擬的網絡裡游戲、社交、狂歡。到了21世紀,我們開始致力於人工智能的開發,而這些東西本質上都是由計算機實現的。在未來,完全身處於數字時代的我們,必將被二進制代碼籠罩。這個世界,1+1就只可能等於2嗎?
結語人類文明的「根」
不管是現實生活中簡單易懂的1+1=2,還是互聯網世界裡的1+1=10,都以其自身的客觀性和普適性在時間長河裡自證「偉大」。1+1=2種下了數學的種子,推動了理性世界的基本運轉。它簡潔美妙,無處不在,是人類文明重要的「根」
補述:
①自然數:用以計量事物的件數或表示事物次序的數,即用數碼0,1,2,3,4…所表示的數。自然數分為偶數和奇數、合數和質數等。② 公理:依據人類理性的不證自明的基本事實,經過人類長期反復實踐的考驗,不需要再加證明的基本命題。一個公理不能被其他公理推導出來(除非有冗余的)。
③ 後繼數:緊接某個自然數後面的一個數,如2的後繼數是3,4的後繼數是5。0不是任何自然數的後繼數,每一個確定的自然數都有一個確定的後繼數。
④ 素數:又稱質數,有無限個,素數定義為在大於1的自然數中,除了1和它本身以外不再有其他因數,即除了1和它本身,不能被其他自然數整除的數。
⑤ 補碼:在計算機系統中,數值一律用補碼來表示和存儲。原因在於,使用補碼可以將符號位和數值域統一處理;同時,加法和減法也可以統一處理。此外,補碼與原碼相互轉換,其運算過程是相同的,不需要額外的硬件電路。
本文 1 1+1=2:數學的溯源(完)
————————————————————————————————2 勾股定理:數與形的結合

人類歷史上第一次把「數」與「形」相結合。

勾三股四弦五
已知一個直角三角形,兩條直角邊長分別為3和4(圖2-1),那麼斜邊的長是多少?

圖2-1 直角三角形
相信你很快就可以得出5這個答案,但最早得出這個答案的人,是我們的祖先商高。在公元前11世紀,商高搶答了這個問題——「勾三股四弦五」。
(待續……)































































































